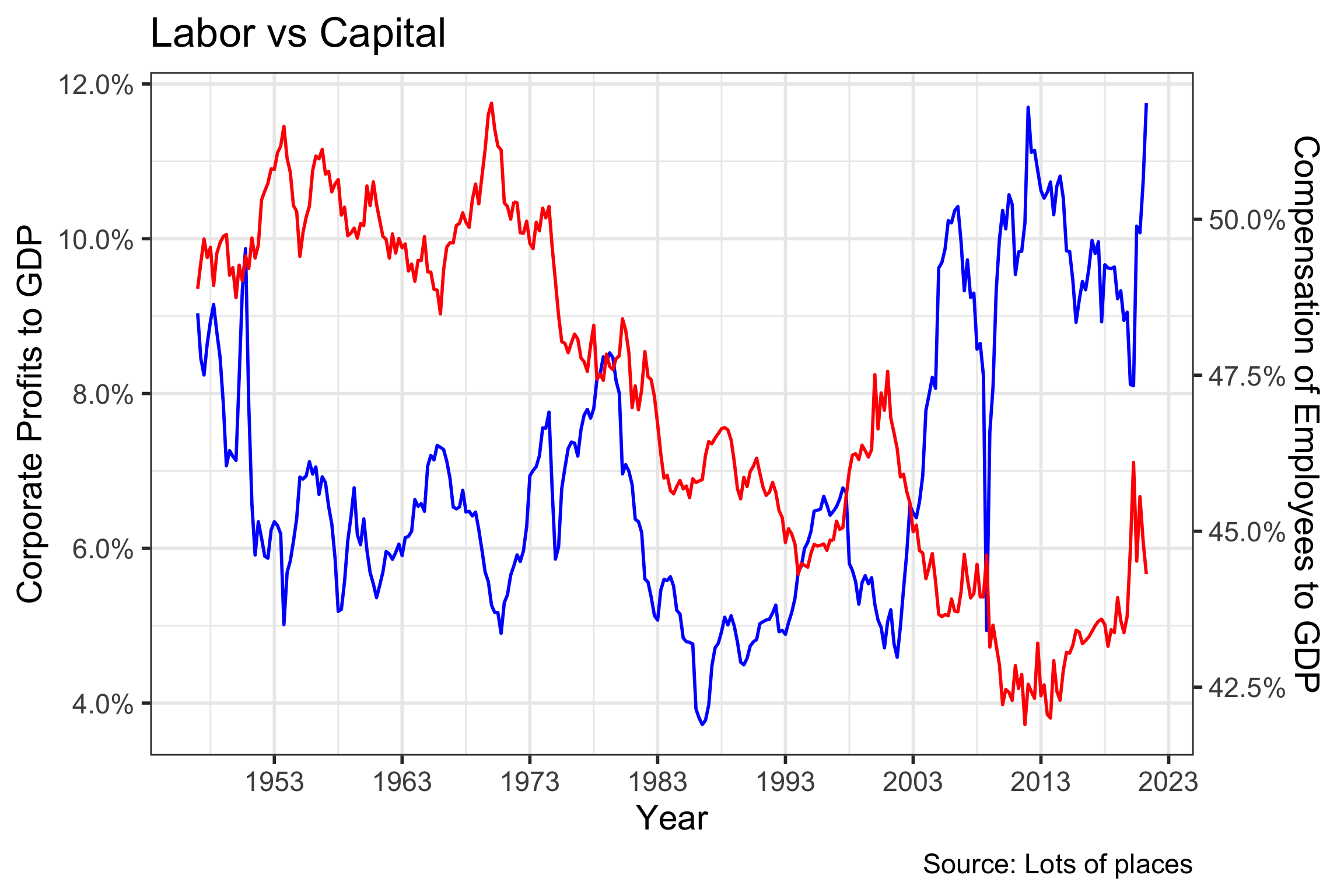
Introduction

The rise in monopoly power particularly in big technology, but possibly, more broadly across the economy and stock market has been a growing topic of conversation in recent years. America’s Monopoly Problem Goes Way Beyond the Tech Giants by David Doyen, and Monopolies Are Distorting the Stock Market, by Kai Wu of Sparkline Capital, one of our favorite data-driven bloggers, are good examples of this thinking. In addition to data on industry concentration, Wu draws the link to discussions over stagnating real wages, and sustained higher profit margins of companies since 1980 in the chart above, which we have seen referenced frequently in the last few years.

When we first heard these arguments, we were skeptical because it seemed like companies had been listing on and departing from exchanges at an accelerating pace, due to globalization and technological change. Industries like media and retailing have seen upheaval, and the departures of many formidable companies, and financial services seems like it could be next. If anything, our perception was that it was becoming more difficult for many incumbents constrained by legacy skills, processes and assets. Many of new listings, usually growing out of the cloud, brought new services we didn’t even know we needed, solved problems not previously addressed or disrupted dominant existing competitors. Spotify, Zoom, Docusign, Shopify, Roblox, Square and Snowflake come to mind as giant companies created in the last 10 years. Even the FAANG stocks of the previous generation are relatively young companies in the context of historical blue chips, and each of these brought us new innovations often at the expense of incumbents.

While still not sure if we are convinced of the monopoly threat, we ran into a possibly related issues in our work analyzing financial statement “red flags”. When we tried to match historical financial statements to subsequent return histories, a surprisingly large number of companies had been de-listed and fallen from data feeds. Once we had acquired the history for most, it was apparent that median, and by an even greater degree, the mean returns of companies trailed the Vanguard TMI (as shown in our Redwall Red Flag Explorer. We would have expected the average stock to do about as well as the collective members of the index, but that has not been the case, suggesting that success has been narrowing to a smaller group of larger enterprises.

How can the creation of promising young digital competitors and shortening lifespans of the average company be squared with the growing monopoly problem narrative? In this post, we will use Sharadar’s coverage to explore stock market listing births and deaths over the measured period. In light of the discourse, we hope to show in this brief post that the shortening of lifespans is undeniable.

Potential for Survivor Analysis with Sharadar Coverage

As discussed in When Yahoo Finance doesn’t have de-listed tickers needed, we chose to go with EOD Historical Data (Disclosure: we get a small credit for referrals), because our needs for now were only one-time, so the cost was substantially lower than the alternatives. However, the coverage spreadsheet of another provider, Sharadar, enabled us to tell exactly which tickers on our list were available in their database prior to investing time to figure out how to navigate the API. Coupled with data manipulation skills, the spreadsheet is a treasure trove of the history of 12,500 listed companies over 35 years, offering the option to explore when most new listings were created and often departed exchanges over several market cycles. Actuaries measure the life expectancy of people and data scientists of customers or website users, so now market watchers can measure the lifespan of an average investment.

An example of the data, we will use is shown in Figure @ref(fig:sharadar-ticker) for a single company. The firstpricedate will most often be when the company listed after going public or spinning off from another, The lastpricedate would generally be when it was purchased by another public or private company, investor or financial sponsor, or otherwise went out of business or stopped being the same legal entity, often though things like tax inversion. We are using the analogy of mortality, but it isn’t the business itself or its assets, but the stock market listing, which we are using as a representation.

# Load data for US and ADR common stocks only with data.table fread
path <- "~/Desktop/David/Projects/new_constructs_targets/"
categories <-
  c(
    "ADR Common Stock",
    "ADR Common Stock Primary Class",
    "Canadian Common Stock",
    "Domestic Common Stock",
    "Domestic Common Stock Primary Class"
  )
sharadar <-
  fread(paste0(path, "data/sharadar_tickers.csv"),
        select = c("permaticker", "category", "sector", "firstpricedate", "lastpricedate", "table", "sicindustry", "scalemarketcap"))
sharadar <- sharadar[
  table == "SEP" & category %chin% categories]

sharadar[permaticker == 122827]

   permaticker              category             sector firstpricedate
1:      122827 Domestic Common Stock Financial Services     1998-09-25
   lastpricedate table            sicindustry scalemarketcap
1:    2003-01-28   SEP State Commercial Banks      2 - Micro

Exploring Security Life and Death with Sharadar’s Coverage

We decided to divide listings into 5 cohorts by firstpricedate: initially listed prior to 1986, between 1986-2001, 2002-2008, 2009-2020, or still alive after that. As shown in Figure @ref(fig:birth-death-table), we noticed that Sharadar’s data shows no de-listings of any companies between 1986 and 1998. In the average year during the 1990s, hundreds tickers were de-listed each year. If that rate was typical, it implies we are probably missing data for thousands tickers which were de-listed between 1986-1998. Based on what we have learned about the difficulty of finding this information, we doubt that any of the providers would have complete information this far back.

# Create first, second and period variables
sharadar[
    , `:=`(
      first = fifelse(
        firstpricedate == "1986-01-01",
        1985,
        year(firstpricedate)), 
      last = fifelse(
        lastpricedate > "2021-06-01",
        2022,
        year(lastpricedate))
    )]

# Generate birth and death periods
sharadar[, `:=`(
  birth_period = fcase(
    first == 1985,
    "Pre-1986",
    first %in% c(1986:2000),
    "1986-2000",
    first %in% c(2001:2008),
    "2001-2008",
    first %in% c(2009:2021),
    "2009-2021",
    default = "missing"
  ),
  death_period = fcase(
    last %in% c(1986:2000),
    "1986-2000",
    last %in% c(2001:2008),
    "2001-2008",
    last %in% c(2009:2021),
    "2009-2021",
    last == 2022,
    "living"
  ))]

# Convert to birth and death tables by period and category (domestic or ADR)
births <-
  sharadar[, .N, 
    .(domestic = re2_detect(category, "Domestic"), 
      period = birth_period)][
        , dcast(
          .SD,
          period ~ domestic,
          fun.aggregate = identity,
          fill = 0)]
setnames(births, c("period", "ADR", "Domestic"))
deaths <-
  sharadar[, .N, 
    .(domestic = re2_detect(category, "Domestic"), 
      period = death_period)][
        , dcast(
          .SD,
          period ~ domestic,
          fun.aggregate = identity,
          fill = 0)]
setnames(deaths, c("period", "ADR", "Domestic"))

# Join together on period
table_list <- list(births, deaths)
table_list <- lapply(table_list, as.data.table)
table_list <- lapply(table_list, setkey, "period")
table <-
  Reduce(function(table1, table2){
    unique_keys <-
      unique(c(table1[, period], table2[, period]))
    table2 <- table2[unique_keys]
    table1[table2, on = "period"]}, table_list)

# Sort by time, rename and reorder
to_ord <- c(4, 1, 2, 3, 5)
table <-
  setorder(table[
    , .r := order(to_ord)], .r)[
      , .r := NULL]
setnames(table,
         c(
           "period",
           "adr_births",
           "dom_births",
           "adr_deaths",
           "dom_deaths"
         ))
setcolorder(table,
            c(
              "period",
              "dom_births",
              "dom_deaths",
              "adr_births",
              "adr_deaths"
            ))

# Make datatable
table <-
  DT::datatable(
    table,
    rownames = FALSE,
    colnames =
      c(
        "Period",
        "Domestic Births",
        "Domestic Deaths",
        "ADR Births",
        "ADR Deaths"
      ),
    options =
      list(pageLength = 5,
           dom = 't')
  ) %>%
  DT::formatRound(
    columns = c(2:5),
    mark = ",",
    digits = 0)

In Figure @ref(fig:history-plot) below, the left panel shows the births of new companies still alive today by sector over time. We can see the high rate that new companies were created during the 1990s (over 500 per year), but also the recent spike driven by the SPAC boom beginning in 2019. We understand that companies have been staying private longer, but the recent surge of “Blank Check” companies shown in blue in the left panel of Figure @ref(fig:history-plot) below, though worrisome, still looks relatively small compared to the 1990s. The fact that new entities have been listed more slowly until recently may not be all bad in light of what we learned of the poor quality listings during the boom.

In addition to fewer companies being listed until recently, our perception has long been that companies are dying at a faster rate because of globalization and technology. As Kai Wu hypothesized in his blog post, many may also have been acquired and/or perished due to stronger global competition and technological advantages. In the second panel, we can see the decline in average lifespan of company listings in all sectors over the period. After giving thought, we realized that younger companies in the data would naturally contribute shorter life spans closer to the end of the measurement period, so this graphic gives a misleading picture. It turns out that there are methods called “survivor analysis” which allows us to see an apples-to-apples picture of the rate of death of companies by cohort. R has the {survivor} package which is built for survival analysis, although we are probably taking liberties using it for non-overlapping periods.

# Build ggplot2 object facets
p <-
    sharadar[
      birth_period != "alive"
      , .(.N, as.integer(round(mean(last - first), digits = 0))),
      .(sector, first)][
        sector != ""
        , melt(.SD, id.vars = c("first", "sector"))][
          , ggplot(.SD, aes(first, value, group = sector, color = sector)) +
            geom_line() +
            facet_wrap( ~ variable, scale = "free_y", 
                        labeller = labeller(variable = 
        c("N" = "Number of Issues",
          "V2" = "Mean Lifespan"))) +
            labs(
              x = "Year"
            ) + 
            theme_bw()]

# Add label title
p$labels$colour <- p$labels$fill <- "Sector"

# Transform to plotly
p <- ggplotly(p)

Coding up Survivor Analysis using the Magic of {data.table}

The data we have from Sharadar is a flat table with one row per company including the first and last listing date. In order to prepare to model with {survivor}, we had to make a relatively complex transformation, creating one row for every company during every year of life. In order to do this, we used a {data.table} (in the first section of the hidden code chunk below), which created a list for every year of life for every ticker, and then “exploded” that list by ticker back into a flat table. We have heard people excited about the Python {Pandas} explode() function, which is dedicated to this purpose. However, we prefer to solve most data wrangling problems using the same generalized toolkit of stable {data.table} functions.

We then had to add the “status” variable denoting if the company was alive with 0, or 1 for the year of death. Sharadar coded companies alive before the beginning of a single date of “1986-01-01”, but all of these companies were not born on that exact date, so it was a place holder for companies born in earlier years. We coded the time period for these years as “1985”, and companies “2022” for companies still alive after June 1, 2021. In order to create the “status” variable, we used the {data.table} elegant .SD (subset of data) filtering. This involved taking the first and last indexed date out of .SD (a kind of an fluid subset of our larger data.frame) by ticker, all using indices within the same code chain.

The last piece of {data.table} code to explain is the final segment, which creates four periods and then a list column of the other data for each of those period. It then merges those lists back into a single data.table including the relevant period. In the {Tidyverse}, this would involve loading {Tidyr} and using its special nest() and unnest() functions for list columns. Again, here we are using the same generalized {data.table} functions instead of a loading another package.

The prevailing school of thought is that the {Tidyverse} is easier to understand and appropriate for smaller data, and that {data.table} has a more complicated syntax, which should be reserved for bigger data. There is a learning curve, but after a couple of years, we feel excitement when approaching this kind of complicated transformation to see the magic of {data.table} solve the problem. In addition to being fastest, {data.table} is also stable without frequent new, specialized functions and changing parameters. Trying to use it only on larger data would probably mean we couldn’t use it to its fullest extent. Finally, we would argue for its elegance over the {Tidyverse}, regardless of data size. After wrangling, the data shown below is for the same ticker we showed above. This company was born in the pre-1986 period and was de-listed within 5 years.

# Create list of data.tables appropriate for survivor modelling
mortality <-
  sharadar[
      sicindustry != "Blank Checks",
    .(permaticker, alive = list(list(first:last))),
    .(first = 
        fifelse(
          firstpricedate != "1986-01-01", 
          year(firstpricedate), 
          1985),
      last = year(lastpricedate))][
        , list(year = unlist(alive)),
        by = permaticker][
          , {
            first = .SD[1]$year
            last = .SD[.N]$year
            time = year - first
            status = fcase(
              year == 2020 & last == 2020,
              1,
              year == 2021 & last == 2021,
              0,
              year < 2020 & year == last,
              1,
              default = 0
            )
            period = fcase(
              first == 1985,
              "Pre-86",
              first %in% c(1986:2000),
              "1986-2000",
              first %in% c(2001:2008),
              "2001-08",
              first %in% c(2009:2020),
              "2009-20",
              default = "missing"
            )
            list(time, status, period)
          }, permaticker][
            period != "missing",
            list(list(.SD)), period]

# Transform lists into a single data.table by period
mortality <- 
  rbindlist(mortality$V1,
            use.names = TRUE,
            fill = TRUE,
            idcol = "period")

# Display transformed mortality data for one company
mortality[permaticker == 122827]

   period permaticker time status
1:      1      122827    0      0
2:      1      122827    1      0
3:      1      122827    2      0
4:      1      122827    3      0
5:      1      122827    4      0
6:      1      122827    5      1

Building the Model and Plotly Object

In this section, we would also like to discuss some coding tricks we have only recently learned about {ggplot2} (which are also effective with {plotly} objects). Given that we have been using these packages so frequently for over four years, it is surprising that it took so long to learn this trick, so it might help others to demonstrate. The {survivor} package has a pre-built function in {ggfortify} to plot Kaplan-Meier (km) objects. The Kaplan-Meier estimate of the survival probability is the product of the conditional probabilities until the event (in this case de-listing). Ordinarily there are treatment groups in a study (ie: treatment and control), but we are pretending that each of the four time periods are separate cohorts in a study.

When we went to view the plot, we found that it was more complicated than we expected to change the legend labels inside the {ggplot2} chain. Thankfully, we can go inside these objects and manually make adjustments after they have been assigned. In the code block, we change the “strata” names to our “period” groups, and now when we run autoplot() on the km object, the labels are fixed. In a similar manner, we manually change the legend title for the color and fill attributes of the list object after we build the autoplot(). Then, the graph shows exactly as we intended.

# Build km object
km <- 
  survfit(
    Surv(time = time, event = status) ~ period, 
    data = mortality)

# Change legend labels
names(km[["strata"]]) <-
  c("Pre-1987", "2009-2021", "2002-2008", "1987-2001")

# Build autoplot
p <- 
  autoplot(km) + 
  theme_bw() + 
  labs(
    title = "Annual Listing Survival Rates by Cohort",
    caption = "Source: Sharadar",
    x = "Age",
    y = "Survival Rate"
  )

# Modify legend title
p$labels$colour <- p$labels$fill <- "Period"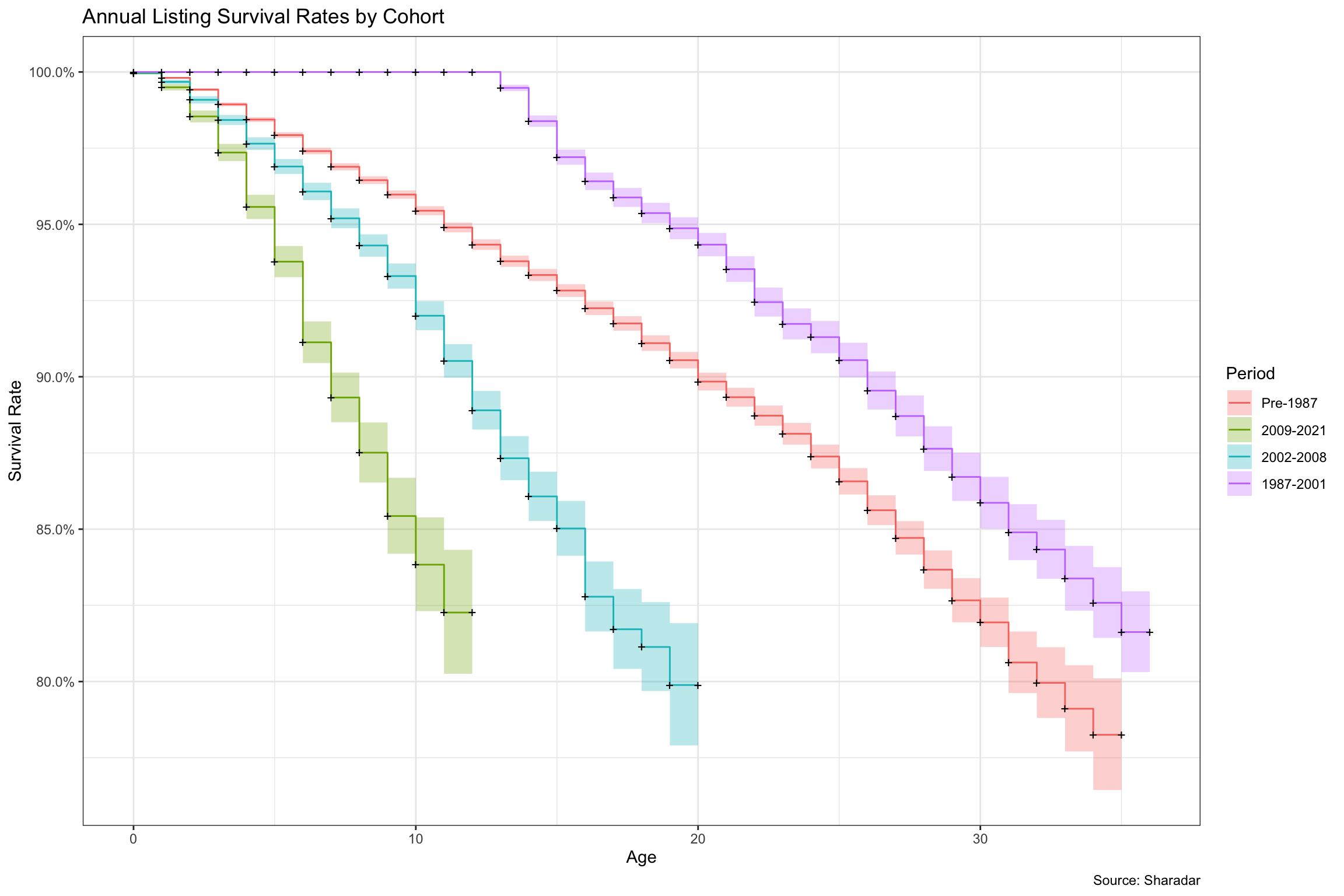

Thoughts on Survival Rates by Period

The top purple estimate (1987-2001) does not actually represent the earliest cohort (pre-1986), but the second in which companies started to be born. The 100% survival rate in the first 12 years of this cohort suggests that the data for de-listings may be missing (and hence also for initial listings). At the same time, we can also see with the red chart (pre-1986), that the rate survival during two early cohorts was surely higher than in the later two periods. The change in the survival rate by year visible in the size of the estimated vertical steps along the y-axis. Once companies start to show de-listings around 1997 (12 years into lives of the companies in that cohort), we can see that the survival rate declines by about 1-2% per year.

The different story starts with companies born in the 2002-2008 cohort, when the survival rate decline is much more rapid. We can see that the years of age are shorter, because every company in the period is measured from its first trading year, and confidence bands are wider, because there are fewer companies included in those cohorts. When the more recent bull market began in the 2009 cohort (green), the survival rate is even lower (even though we have actually removed the most recent surge in SPAC issuance). It also seems that the rate of de-listing for the earlier groups also accelerates around the same time as the later cohorts start. Looking at the x-axis from right to left allows to see comparable periods, and interestingly, the most recent cohort appears like it will soon catch up to the others, even though it started 12 years after then next latest. All in all, about 20% of companies for all of the cohorts have been de-listed.

Conclusion

We may have taken liberties using different time cohorts as treatment, but seemed like a better than the alternative of including them all in one group. Our analysis doesn’t help at all to understand the causes of or possible remedies for the shortening life of listings, or if it is even good or bad. Shortening lifespans of companies may be caused by the predatory behavior of monopolies, accelerating obsolescence of enterprises, Dodd-Frank raising the cost of listing, tax inversions, or some other combination of factors. Although as guilty as any of throwing up charts on this blog and speculating over what they might signify, we will not attempt to do so here. Suffice it to say that it listing lives have shortened, and we will leave it for others to explain the true causes.